Research, Stepan Malkov

Anderson Localization

One of the characteristic features of classical particle models is the prominence of diffusive behavior. An individual particle’s behavior in a random potential $V$ exhibits Brownian motion, and the distribution of an ensemble of particles evolves according to the diffusion equation $u_t(x,t) = \nabla \cdot [V(x) \nabla u(x,t)].$

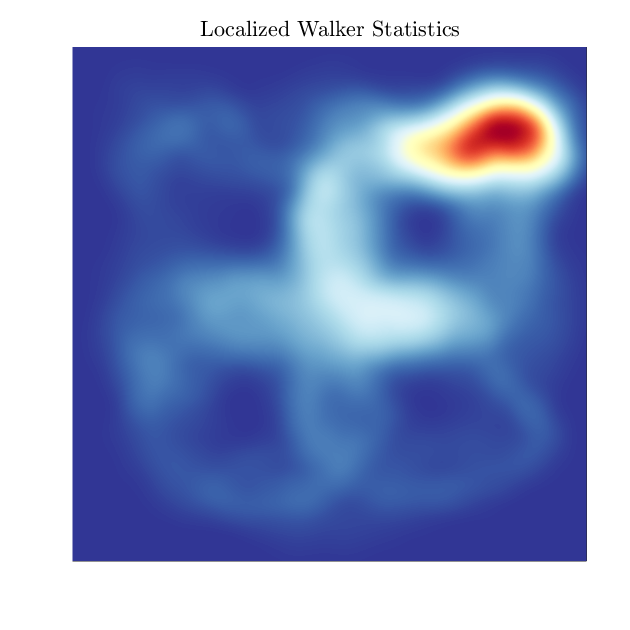
In stark contrast to the classical case, quantum wavefunctions evolving according to the Schrödinger equation are able to demonstrate a lack of diffusion in sufficiently disordered potentials, a phenomenon known as Anderson localization. We demonstrate that such behavior can be rationalized through a classical wave-particle model known as walking droplets, showing localization of walker statistics highly reminiscent of Anderson localization in a over a bath containing a submerged disordered topography.

By combining experiments and simulations, we show that the walker, which is propelled by its own wavefield over the submerged topography, “prefers” a particular region of the topography, which is characterized by a peak in its trajectory histogram, bearing a notable resemblance to the dominant eigenmode of the Schrödinger equation for the same potential. Moreover, we suggest a mechanism for walker localization driven by the nonlocal interaction of the underlying waves guiding the droplet.

The proposed hydrodynamic quantum analogue opens up novel and interesting connections between classical physics and the underlying wave-particle duality of subatomic particles, suggesting other quantum phenomena, such as the Aharonov-Bohm effect, as potential directions for future research.

UPDATE 11/24: Our paper has been published in Physical Review X! Abraham, A. J., Malkov, S., Ljubetic, F. A., Durey, M., & Sáenz, P. J. (2024). Anderson Localization of walking droplets. Physical Review X, 14(3). https://doi.org/10.1103/physrevx.14.031047

This research is conducted in affiliation with Physical Mathematical Laboratory (PML) at UNC-Chapel Hill.

Decay Estimates for the Haldane-Lieb Hamiltonian

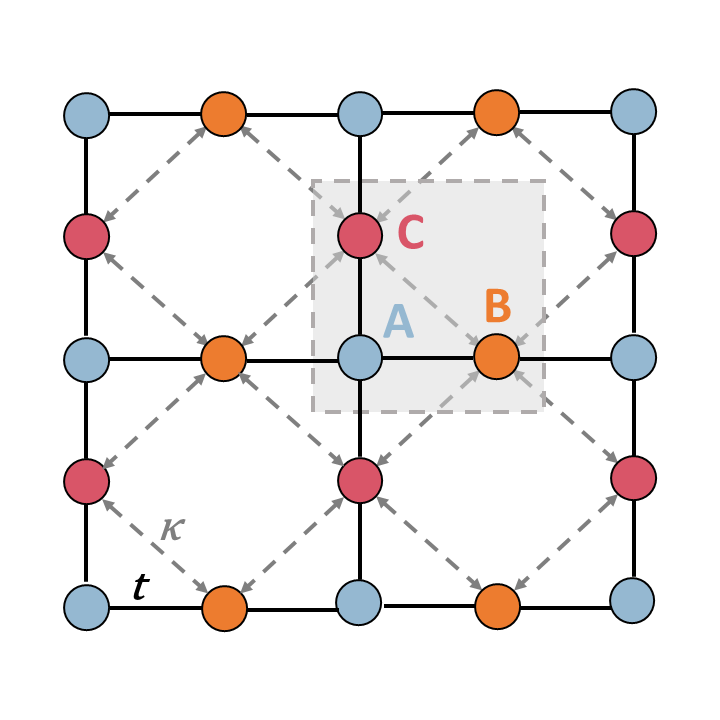
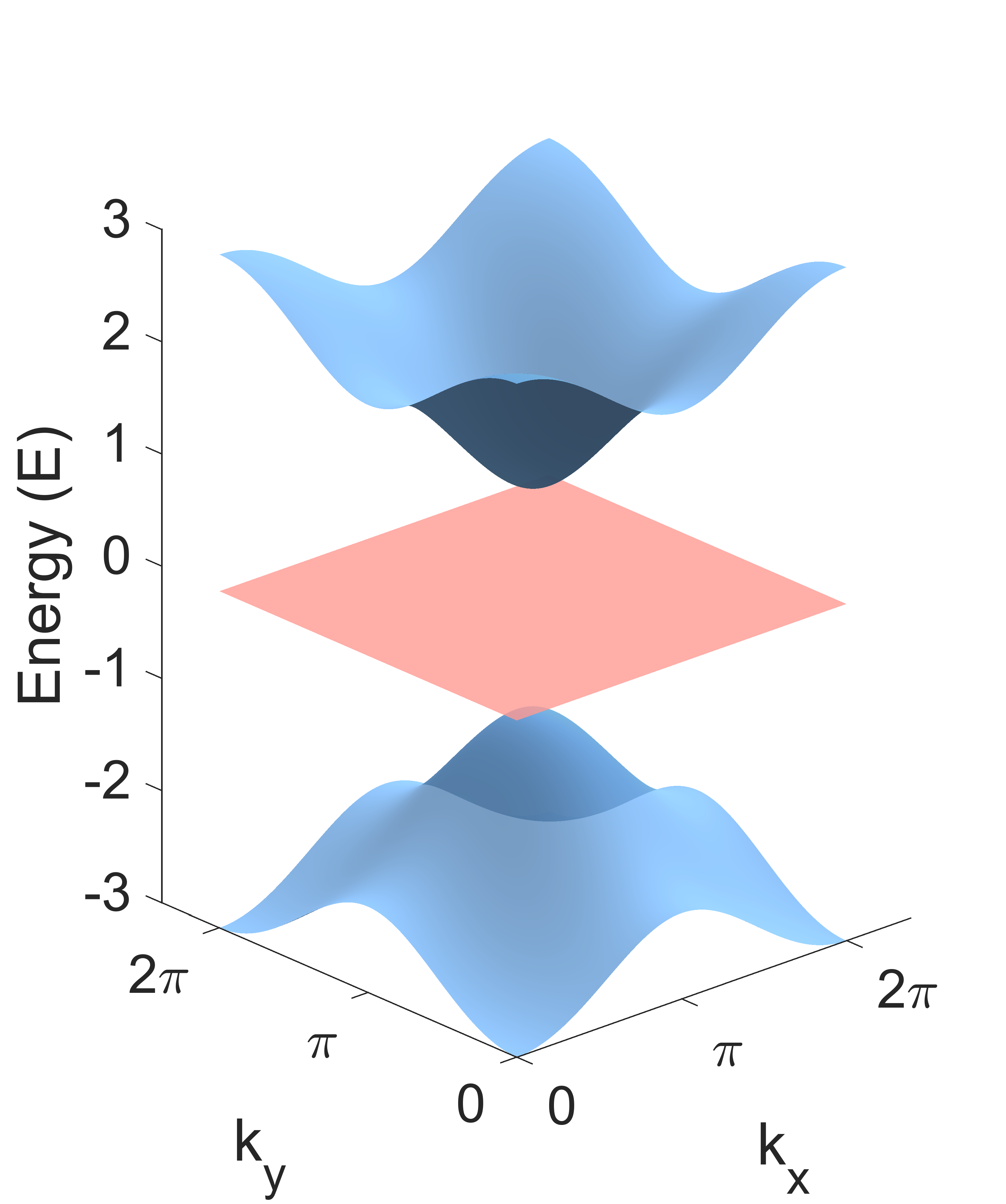
One of the biggest modern advancements in solid-state physics is the discovery of certain topological properties of quantum systems that directly characterize behavior. Such topological phenomena, such as the well-known the Quantum Hall Effect (QHE), crucially depend on the range of possible energies of a system, known as the system’s spectrum. In particular, if we consider the Lieb lattice (shown on the right), its spectrum is characterized by a topological band gap, a range of forbidden energies.

Yet, if one adds forcing to the system in the form of a nonlinearity, one is able to obtain solutions inside the gap, forcing them to decay exponentially at infinity. By relying on spectral techniques, we are able to show exponential decay of nonlinear states on the Lieb lattice, with decay rate directly proportional to the distance from the edge of the gap. Moreover, by a suitable ansatz, we are able to obtain a coupled system of ODEs, which we analyze using classical shooting techniques. Finally, we use numerical methods to predict the structure of linear and nonlinear states and justify the radial ansatz for the nonlinear system.

This work was completed as part of a senior honors thesis defense under the mentorship of Dr. Jeremy Marzuola at UNC-Chapel Hill.