Since we now know that a power series defines a continuous function within its region of convergence, one might wonder if the reverse is true, i.e. if any continuous function can be written as a power series. This is where Taylor series prove to be extremely useful.
Definition:
For a continuous function
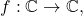
define its
Taylor series expansion around 
to be the power series
![Rendered by QuickLaTeX.com \[f(z) = \sum_{n=0} a_n (z-a)^n,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-2c43974a7dfa2d2dc24eec1f27120244_l3.png)
where
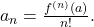
Then, the Taylor series for

is the unique power series representation for

at

that converges to

inside
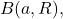
where
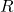
is the radius of convergence.
Examples:
Recall that the Taylor series for
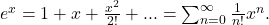
Thus, one defines the
complex exponential
![Rendered by QuickLaTeX.com \[e^z = \sum_{n=0}^\infty \frac{1}{n!},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-712719be1e8dd474ff02dc214a835c9e_l3.png)
with radius of convergence that can be determined by the root test to be
![Rendered by QuickLaTeX.com \[\lim_{n \to \infty} \frac{\frac{1}{n!}}{\frac{1}{(n+1)!}} = \lim_{n \to \infty} n+1 = \infty.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-3060b717844a491e89dc38b9a503b267_l3.png)
Thus, the power series converges everywhere on the complex plane to
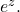
The function obeys the same properties as the real exponential, namely,
![Rendered by QuickLaTeX.com \[e^{z_1+z_2} = e^{z_1}e^{z_2}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-68e60bde8bd32cb73d3af2c1dc35b358_l3.png)
The
complex logarithm can be similarly defined as
![Rendered by QuickLaTeX.com \[\log (1-z) = \sum_{n=1}^\infty \frac{z^n}{n},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-26b23241421de3d8ef69984d5f14c4d6_l3.png)
which converges for
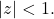
Similarly, one defines complex sine and cosine through their power series to be
![Rendered by QuickLaTeX.com \[\sin z = \sum_{n=0}^\infty \frac{(-1)^{n+1} z^{2n+1}}{(2n+1)!}, \cos z = \sum_{n=0}^\infty \frac{(-1)^n z^{2n}}{(2n)!},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5b71e10e9ef4db8371ceecf18c4444f9_l3.png)
which can also be checked to converge everywhere on
One is then also able to derive Euler’s formula using
![Rendered by QuickLaTeX.com \[r(\cos \theta + i \sin \theta) = r\left(\sum_{n=0}^\infty \frac{(-1)^{n+1} \theta^{2n+1}}{(2n+1)!} + i\sum_{n=0}^\infty \frac{(-1)^n \theta^{2n}}{(2n)!}\right) = r\sum_{n=0}^\infty \frac{(i\theta)^n}{n!} = re^{i \theta}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-93bad7b75990d5cc711c01e8810353fd_l3.png)
We noticed that a power series defines a continuous function, but is that function differentiable, and if so, how many derivatives can you take? What about integration?
Proposition:
Suppose
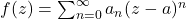
is a complex power series with radius of convergence
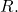
Then, for any

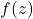
is differentiable and Riemann integrable on
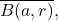
with
![Rendered by QuickLaTeX.com \[f'(z) = \sum_{n=1}^\infty n a_n (z-a)^{n-1}, \quad \int_a^z f(y) dy = \sum_{n=0}^\infty a_n \frac{(z-a)^{n+1}}{n+1}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-16ac420ca1f0305c1cdb42e9d078b445_l3.png)
Proof:
Note that the radius of convergence for both series is the same
![Rendered by QuickLaTeX.com \[R=\frac{1}{\limsup_{n \to \infty}|a_n|^{\frac{1}{n}}}=\frac{1}{\limsup_{n \to \infty} |na_n|^{\frac{1}{n}}} = \frac{1}{\limsup_{n \to \infty} |\frac{a_n}{n+1}|^{\frac{1}{n}}},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b6c476959675f444375577a7b90d8087_l3.png)
since
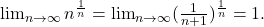
For the Riemann integral of
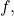
we use the fact that the uniform limit of Riemann integrable functions is Riemann integrable, obtaining that the power series
![Rendered by QuickLaTeX.com \[\sum_{n=0}^k \int_a^z a_n (y-a)^n dy = \int_a^z \sum_{n=0}^k a_n (y-a)^n dy \to \int \sum_{n=0}^\infty a_n (y-a)^n dy = \int_a^z f(y)dy,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-4b0af9673bb05db878a57845a4e801b0_l3.png)
i.e.
![Rendered by QuickLaTeX.com \[\sum_{n=0}^\infty a_n \frac{(z-a)^{n+1}}{n+1} = \int_a^z f(y) dy.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f7273ea9cd4225a6337bd5556f1e04db_l3.png)
For the derivative of
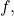
we use Theorem 3.7.1 in the textbook, which states that if
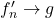
uniformly and
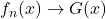
for at least one
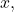
then
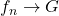
uniformly,
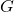
is differentiable, and
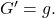
Note that the first part of the theorem follows immediately from the uniform convergence for the Riemann integral and an application of the Fundamental Theorem of Calculus. We note that the derivative series converges uniformly to some function
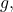
and the series for

converges for at least one point in the region of convergence, so by applying Theorem 3.7.1, we get that

is differentiable with
![Rendered by QuickLaTeX.com \[g(z) = f'(z) \quad \forall z \in \overline{B(a,r)}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-65c6499d8c12535402c7c3eb41124ddf_l3.png)
Corollary:
Any power series defines an infinitely differentiable function, all of whose derivatives are continuous and which converge uniformly in the same region of convergence (such functions are called smooth or
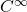
functions).
Remark:
A natural question to ask is whether all smooth functions can be defined by a power series. Surprisingly, the answer is no. For example, the function
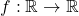
given by
![Rendered by QuickLaTeX.com \[f(x) = \begin{cases} e^{-\frac{1}{x}}, & x > 0 \\ 0, & x<0\\ \end{cases}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ea488f36f83a66ad118c089667cb8303_l3.png)
is smooth but its Taylor series at
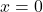
has radius of convergence 0.
However, power series precisely correspond to functions that are “smooth” in the complex plane, called holomorphic functions, which satisfy very peculiar and nice properties and are beyond the scope of this course.
Finally, I want to state a test (without proof) that lets one check the continuity of a power series on the boundary of the region of convergence, known as Abel’s Test.
Theorem (Abel’s Test):
Let
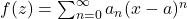
be a real power series with radius of convergence
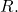
If the power series converges for some
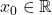
such that
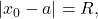
then

is continuous at

![]()
![]()
![Rendered by QuickLaTeX.com \[\lim_{n \to \infty} \frac{\frac{1}{n!}}{\frac{1}{(n+1)!}} = \lim_{n \to \infty} n+1 = \infty.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-3060b717844a491e89dc38b9a503b267_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[r(\cos \theta + i \sin \theta) = r\left(\sum_{n=0}^\infty \frac{(-1)^{n+1} \theta^{2n+1}}{(2n+1)!} + i\sum_{n=0}^\infty \frac{(-1)^n \theta^{2n}}{(2n)!}\right) = r\sum_{n=0}^\infty \frac{(i\theta)^n}{n!} = re^{i \theta}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-93bad7b75990d5cc711c01e8810353fd_l3.png)
![Rendered by QuickLaTeX.com \[f'(z) = \sum_{n=1}^\infty n a_n (z-a)^{n-1}, \quad \int_a^z f(y) dy = \sum_{n=0}^\infty a_n \frac{(z-a)^{n+1}}{n+1}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-16ac420ca1f0305c1cdb42e9d078b445_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\sum_{n=0}^k \int_a^z a_n (y-a)^n dy = \int_a^z \sum_{n=0}^k a_n (y-a)^n dy \to \int \sum_{n=0}^\infty a_n (y-a)^n dy = \int_a^z f(y)dy,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-4b0af9673bb05db878a57845a4e801b0_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[f(x) = \begin{cases} e^{-\frac{1}{x}}, & x > 0 \\ 0, & x<0\\ \end{cases}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ea488f36f83a66ad118c089667cb8303_l3.png)