Compactness and Completeness
Recall that a sequence
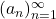
is
Cauchy if for every
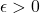
there exists an
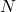
such that
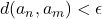
whenever
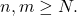
Today, we will cover compact, sequentially compact, and complete metric spaces.
Definition:
A metric space
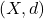
is called
compact if for any collection of open sets
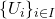
such that
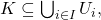
there exist

such that
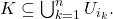
In other words, every open cover has a finite subcover. If
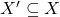
and
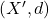
is compact, we call the set
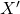
compact.
Definition
A metric space
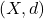
is called
sequentially compact if every sequence has a convergent subsequence with its limit in
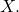
If
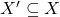
and
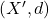
is compact, we call the set
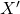
compact.
Definition:
A metric space
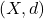
is called \textbf{complete} if every Cauchy sequence has a limit in
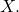
We consider several examples of compact and complete sets.
Example:
- Any closed and bounded subset of
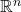 is compact. As we will show later today, every compact set in
is compact. As we will show later today, every compact set in 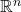 is closed and bounded.
is closed and bounded.
- Any metric space
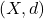 where
where  has finitely many elements is compact.
has finitely many elements is compact.
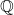 with the usual metric is not complete. Let
with the usual metric is not complete. Let  where
where 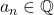 gives the first
gives the first 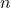 digits of
digits of  Then,
Then, 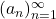 is Cauchy but does not converge to an element in
is Cauchy but does not converge to an element in 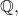 i.e.
i.e. 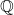 is not complete.
is not complete.![Rendered by QuickLaTeX.com C([a,b])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f35be6e11d9032f8085c0fd0db284b45_l3.png) with the metric of uniform convergence is complete, since continuous functions on a closed and bounded interval are uniformly continuous, and the limit of a uniformly convergent sequence is uniformly continuous.
with the metric of uniform convergence is complete, since continuous functions on a closed and bounded interval are uniformly continuous, and the limit of a uniformly convergent sequence is uniformly continuous.
We now prove some important results that relate these three categories.
Proposition
A set

in a metric space
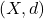
is compact if and only if it is sequentially compact.
Proof:
(

) Suppose

is compact, and let
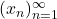
be a sequence in
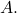
Note that
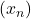
has a convergent subsequence in

if and only if there is an
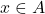
that is a limit point of
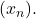
For sake of contradiction, suppose the sequence has no limit points. Then, for every
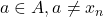
for some
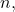
there exist an
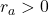
such that
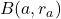
contains no elements of the sequence, and for each
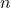
there exists an
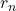
such that
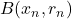
does not contain any element of the sequence other than
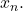
But then, if
![Rendered by QuickLaTeX.com \[U=\bigcup_{a \in A \setminus \{x_1,x_2,...\}} B(a,r_a), \quad V= \bigcup_{n} B(x_n,r_n),\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9acb0b7141b51f3bd06187e8428c5bf1_l3.png)
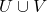
is an open cover of
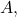
so it has a finite subcover
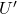
. Note that for all
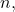
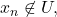
and since the subcover
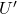
is finite, there exists an
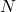
such that
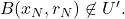
But by construction, this implies
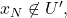
so
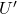
does not cover
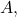
which is a contradiction.
(

) Suppose

is sequentially compact.
We first show that there exists an
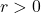
such that for every
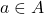
and every open cover
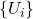
of
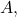
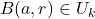
for some
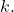
Suppose there isn’t such a
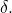
Then, for every
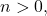
there exists an
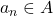
such that
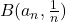
is not fully contained in any
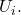
Extract a convergent subsequence
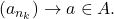
Then,
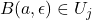
for some

But for
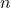
such that
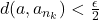
and

![Rendered by QuickLaTeX.com \[B\left(a_{n_k},\frac{1}{n_k}\right) \subseteq B(a,\epsilon) \subseteq U_j,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-91a6ef268a4dca9ca3ae4b633775842a_l3.png)
which is a contradiction.
Now, suppose there exists an open cover
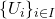
of

which does not have a finite subcover. Using the lemma, pick
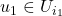
such that for some
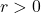
,
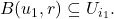
Since
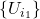
is finite, it does not cover
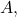
so there is a
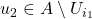
with
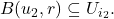
Proceeding in this fashion, we construct a sequence of elements
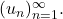
Then, since
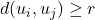
for all
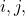
no subsequence of
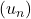
is Cauchy, so no subsequence of
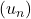
converges, which is a contradiction.
Proposition
A compact set
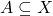
is closed, bounded, and complete.
Proof:
Completeness is easy: if for all
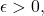
there exist
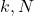
such that
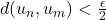
for
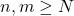
and
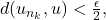
then
![Rendered by QuickLaTeX.com \[d(u_n,u) \leq d(u_n,u_{n_k}) + d(u_{n_k},u) < \epsilon\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-57c66bf210b06a1be069de0eae5d1206_l3.png)
for
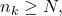
so
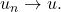
Similarly, if
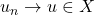
and
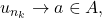
then
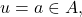
i.e.

is closed. If

is not bounded, it is possible to construct a sequence
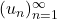
such that
![Rendered by QuickLaTeX.com \[u_n \in B(x,r_{n+1}) \setminus B(x,r_n)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5b0be6032f494652db0bf5d74524bd25_l3.png)
for some
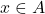
and
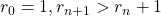
for all
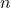
(otherwise,

would be bounded). Then,
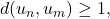
so
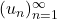
has no convergent subsequence, i.e.

is not compact.
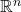 is compact. As we will show later today, every compact set in
is compact. As we will show later today, every compact set in 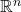 is closed and bounded.
is closed and bounded.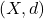 where
where  has finitely many elements is compact.
has finitely many elements is compact.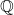 with the usual metric is not complete. Let
with the usual metric is not complete. Let  where
where 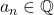 gives the first
gives the first 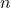 digits of
digits of  Then,
Then, 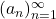 is Cauchy but does not converge to an element in
is Cauchy but does not converge to an element in  i.e.
i.e.  is not complete.
is not complete.![Rendered by QuickLaTeX.com C([a,b])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f35be6e11d9032f8085c0fd0db284b45_l3.png) with the metric of uniform convergence is complete, since continuous functions on a closed and bounded interval are uniformly continuous, and the limit of a uniformly convergent sequence is uniformly continuous.
with the metric of uniform convergence is complete, since continuous functions on a closed and bounded interval are uniformly continuous, and the limit of a uniformly convergent sequence is uniformly continuous.![]()
![]()
![]()
![]()