Open and Closed Sets
We review the definitions of open and closed sets.
Definition:
A subset
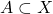
of a metric space is said to be
open if it contains none of its boundary points, i.e
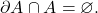

is said to be
closed if it contains all of its boundary points, i.e.

Proposition:
The following are equivalent definitions of an open set:
-
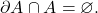
- For any
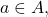 there exists an
there exists an 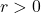 such that the open ball
such that the open ball 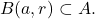
-
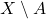 is closed.
is closed.
Proof
(1)

(2): Let
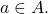
Then,
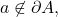
i.e.
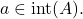
But this means precisely that there exists an
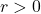
such that
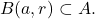
(2)

(3): Let
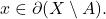
Then, for any
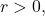
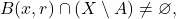
so
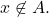
But then,
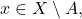
i.e.
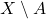
is closed.
(3)

(1): let
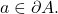
Then, for any
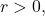
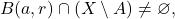
i.e.
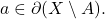
But since
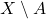
is closed, this implies that
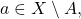
so
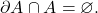
Proposition:

is closed if and only if for any sequence
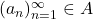
such that
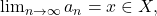
it follows that
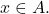
Proof:
Suppose

is closed, and let
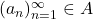
be a sequence such that
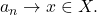
Then, either
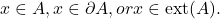
If
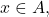
we are done. If
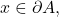
since
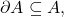
we are also done. If
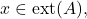
there exists an
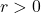
such that
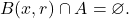
But this contradicts the fact that
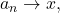
since for any
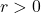
one can find an
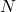
such that
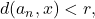
i.e.
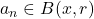
for

Conversely, suppose that
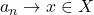
implies
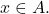
Let
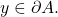
Want to show
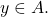
But for any
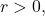

i.e. can find an element
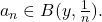
Then,
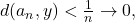
so
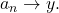
But this implies
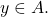
Thus,

is closed.
Proposition:
An arbitrary union (finite intersection) of open sets is open. An arbitrary intersection (finite union) of closed sets is closed.
Examples:
- Any closed interval is a closed set in
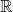 and any open interval is an open set in
and any open interval is an open set in 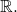
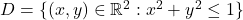 is closed in
is closed in 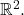
- Let
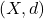 be any set with the discrete metric. Then, any subset
be any set with the discrete metric. Then, any subset  is closed and open.
is closed and open.
- Let
![Rendered by QuickLaTeX.com C([a,b])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f35be6e11d9032f8085c0fd0db284b45_l3.png) be the space of continuous functions on the interval
be the space of continuous functions on the interval ![Rendered by QuickLaTeX.com [a,b]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) with the metric
with the metric ![Rendered by QuickLaTeX.com d(f,g) = \sup_{x \in [a,b]} |f(x)-g(x)|](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5b9495d298ed10896a127fe356e6d6e5_l3.png) (exercise to verify this is inded a metric). Then, the set
(exercise to verify this is inded a metric). Then, the set
![Rendered by QuickLaTeX.com \[X = \{f \in C([a,b]): f(a) = 0\}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-97532c6a80fcf0e1727b53c9bc402715_l3.png)
is closed but not open, for 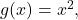
![Rendered by QuickLaTeX.com \[Y = \{f \in C([a,b]): \sup_{x \in [a,b]}|f(x)-x^2|<1\} = B(g,1)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f5c22f7bf7a14dded101e5d5f9a3f9a0_l3.png)
is open but not closed,
![Rendered by QuickLaTeX.com \[Z = \{f \in C([a,b]): f(a)<f(b)\}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-90b858b323f7b36828b2d1eee46caf82_l3.png)
is neither closed nor open.
- In
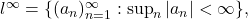 the space of bounded sequences, the subset
the space of bounded sequences, the subset 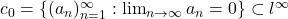 is closed but not open.
is closed but not open.
As seen by the previous example, note that a set being not closed
does not imply that it is open. Thus, sets can be closed, open, both, or neither. An example of a set in
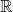
that is neither closed nor open in
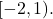
However, the only sets in a subset

with the induced metric that are both closed and open are the empty set
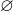
(trivially), and the entire subspace
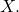
Definition:
Let
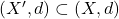
be a subspace with the induced metric. Then,
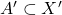
is open (closed) in
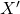
if there exists an open (closed) set
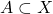
such that
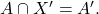
Example:
Take
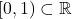
with the induced metric. Then,
![Rendered by QuickLaTeX.com [0,\frac{1}{2}]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b0561769bbd925cb69651e7114a53951_l3.png)
is closed but not open,
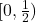
is open but not closed, and
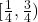
is neither open nor closed. The only sets in
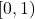
that are both open and closed are
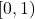
and

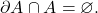
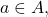 there exists an
there exists an 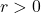 such that the open ball
such that the open ball 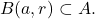
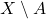 is closed.
is closed.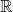 and any open interval is an open set in
and any open interval is an open set in 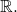
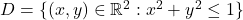 is closed in
is closed in 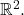
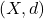 be any set with the discrete metric. Then, any subset
be any set with the discrete metric. Then, any subset  is closed and open.
is closed and open.![Rendered by QuickLaTeX.com C([a,b])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f35be6e11d9032f8085c0fd0db284b45_l3.png) be the space of continuous functions on the interval
be the space of continuous functions on the interval ![Rendered by QuickLaTeX.com [a,b]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) with the metric
with the metric ![Rendered by QuickLaTeX.com d(f,g) = \sup_{x \in [a,b]} |f(x)-g(x)|](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5b9495d298ed10896a127fe356e6d6e5_l3.png) (exercise to verify this is inded a metric). Then, the set
(exercise to verify this is inded a metric). Then, the set
![Rendered by QuickLaTeX.com \[X = \{f \in C([a,b]): f(a) = 0\}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-97532c6a80fcf0e1727b53c9bc402715_l3.png)
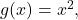
![Rendered by QuickLaTeX.com \[Y = \{f \in C([a,b]): \sup_{x \in [a,b]}|f(x)-x^2|<1\} = B(g,1)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f5c22f7bf7a14dded101e5d5f9a3f9a0_l3.png)
![Rendered by QuickLaTeX.com \[Z = \{f \in C([a,b]): f(a)<f(b)\}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-90b858b323f7b36828b2d1eee46caf82_l3.png)
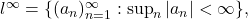 the space of bounded sequences, the subset
the space of bounded sequences, the subset 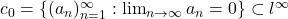 is closed but not open.
is closed but not open.