Today’s problem appeared as Problem 9 on Stanford’s Spring 2017 Analysis Qual:
Problem 9. Suppose  with non-negative imaginary part is such that
with non-negative imaginary part is such that 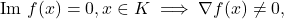 where
where 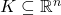 is some compact set. Show that for all
is some compact set. Show that for all 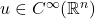 with support in
with support in 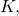 for all
for all  there exists a
there exists a 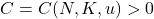 such that
such that
![Rendered by QuickLaTeX.com \[\left|\int e^{i \omega f(x)} u(x)dx\right| \leq C \omega^{-N}, \quad \omega >1.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-20243ab28dd7d867f1c8aa0b02cb0e9f_l3.png)
Solution: Split the integral over the part where the imaginary part of  is at least
is at least  and less than
and less than  for some small
for some small  If
If 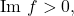 then
then  as
as 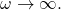 In particular, the decay is exponential, i.e. since
In particular, the decay is exponential, i.e. since 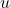 is smooth and compactly supported, one has
is smooth and compactly supported, one has
![Rendered by QuickLaTeX.com \[|e^{i \omega f(x)} u(x)| \leq e^{-\epsilon \omega} \|u\|_\infty = C(K,u) e^{-\epsilon \omega} \leq C(K,u,N,\epsilon) \omega^{-N}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-71d19923b0465fbce3a8f366e17d4a42_l3.png)
for all

(since exponential decay is faster than algebraic decay). Now, when
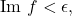
we note that near a point
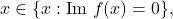
we have the Taylor series approximation
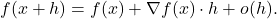
It follows that
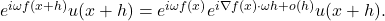
By performing a change of variables to integrate locally in
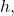
using a compactness argument to select finitely many center points, and shrinking

enough to control the error term in Taylor’s theorem at each center point, we thus get that
![Rendered by QuickLaTeX.com \[\int_{\text{Im}f(x+h)<\epsilon} e^{i\omega f(x+h)}u(x+h) dh \sim \widehat{v}(-\omega (\nabla f(x)+f(x)))+o(h),\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-2fbecc2cc6941c83b7f23f0b9baa777e_l3.png)
where
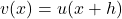
and
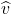
is the Fourier transform of
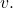
Now, since

is smooth and compactly supported, by the properties of the Fourier transform, one has that
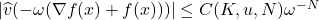
for all
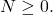
It follows that by sending
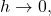
one gets
![Rendered by QuickLaTeX.com \[\int e^{i \omega f(x)} u(x)dx = \int_{\text{Im }f > \epsilon} e^{i \omega f(x)} u(x)dx +\int_{\text{Im }f \leq \epsilon} e^{i \omega f(x)} u(x)dx \lesssim C(u,N,K) \omega^{-N}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-46df9cd86fc5f098ab8aa54e83ef81f3_l3.png)
as
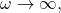
which demonstrates the desired claim.
![]() with non-negative imaginary part is such that
with non-negative imaginary part is such that ![]() where
where ![]() is some compact set. Show that for all
is some compact set. Show that for all ![]() with support in
with support in ![]() for all
for all ![]() there exists a
there exists a ![]() such that
such that ![]()
![]() is at least
is at least ![]() and less than
and less than ![]() for some small
for some small ![]() If
If ![]() then
then ![]() as
as ![]() In particular, the decay is exponential, i.e. since
In particular, the decay is exponential, i.e. since ![]() is smooth and compactly supported, one has
is smooth and compactly supported, one has ![]()
![]()
![]()