Today’s problem appeared as Problem 1 on the UCLA Fall 2019 Analysis Qual:
Problem 1. Given 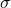 -finite measures
-finite measures 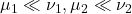 on a measure space
on a measure space 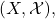 prove that the product measures
prove that the product measures 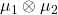 and
and 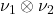 on
on 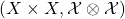 satisfy
satisfy 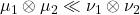 and
and
![Rendered by QuickLaTeX.com \[\frac{d(\mu_1 \otimes \mu_2)}{d(\nu_1 \otimes \nu_2)} (x,y)= \frac{d\mu_1}{d\nu_1} (x) \frac{d\mu_2}{d\nu_2} (y)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b8c1b53d65a31a0e9a1ac414f5a13f79_l3.png)
in the sense of Radon-Nikodym derivatives
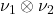
-a.e.
Solution: It suffices to show the representation formula, since it would imply the absolute continuity of the product measures. Since 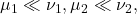 the Radon-Nikodym derivatives
the Radon-Nikodym derivatives  are well-defined and
are well-defined and
![Rendered by QuickLaTeX.com \[\int \chi_A(x) \chi_B(y)d\mu_1(x)d\mu_2(y) = (\mu_1 \otimes \mu_2)(A \times B) = \mu_1(A)\mu_2(B) =\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f5fa5f812cd15b4be7ce35945b19d924_l3.png)
![Rendered by QuickLaTeX.com \[\int \chi_A (x)\frac{d\mu_1}{d\nu_1} (x)d\nu_1(x) \int \chi_B (y) \frac{d\mu_2}{d\nu_2}(y) d\nu_2(y)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-a211c8bd2f7a7b6d694ac35eff19ef73_l3.png)
![Rendered by QuickLaTeX.com \[= \int \chi_A(x)\chi_B(y) \frac{d\mu_1}{d\nu_1}(x)\frac{d\mu_2}{d\nu_2}(y)d\nu_1(x)d\nu_2(y),\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9e54c9f29cac4580dd74c2645d41e677_l3.png)
which implies that the representation formula holds valid on rectangles of the form
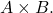
We know by the Caratheodory construction that any
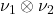
-measurable set
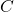
may be approximated in measure by a countable union of such rectangles. Since characteristic functions of finite unions and intersections of rectangles can be written as a finite disjoint sum of rectangles, it follows by linearity that we can approximate the characteristic function of an arbitrary measurable set by a linear combination of characteristic functions of rectangles. Finally, since the representation formula holds for rectangles, by a density argument we extend the formula to hold for characteristic functions of measurable sets. But this precisely implies that
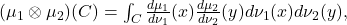
so
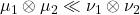
and the desired equality holds
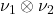
-a.e.
![]() -finite measures
-finite measures ![]() on a measure space
on a measure space ![]() prove that the product measures
prove that the product measures ![]() and
and ![]() on
on ![]() satisfy
satisfy ![]() and
and ![]()
![]() the Radon-Nikodym derivatives
the Radon-Nikodym derivatives ![]() are well-defined and
are well-defined and ![]()
![]()
![]()